Edmonds' algorithm
In graph theory, a branch of mathematics, Edmonds' algorithm or Chu–Liu/Edmonds' algorithm is an algorithm for finding a maximum or minimum optimum branchings. When nodes are connected by weighted edges that are directed, a minimum spanning tree algorithm cannot be used. Instead an optimum branching algorithm should be applied using the algorithm proposed independently first by Yoeng-jin Chu and Tseng-hong Liu (1965) and then by Edmonds (1967). To find a maximum path length, the largest edge value is found and connected between the two nodes, then the next largest value, and so on. If an edge creates a loop, it is erased. A minimum path length is found by starting from the smallest value.
Contents |
Order
The order of this algorithm is 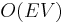 . There is a faster implementation of the algorithm by Robert Tarjan. The order is
. There is a faster implementation of the algorithm by Robert Tarjan. The order is 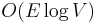 for a sparse graph and
for a sparse graph and 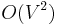 for a dense graph. This is as fast as Prim's algorithm for an undirected minimum spanning tree. In 1986, Gabow, Galil, Spencer, and Tarjan made a faster implementation, and its order is
for a dense graph. This is as fast as Prim's algorithm for an undirected minimum spanning tree. In 1986, Gabow, Galil, Spencer, and Tarjan made a faster implementation, and its order is 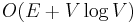 .
.
Algorithm
Description
The algorithm has a conceptual recursive description. We will denote by  the function which, given a weighted directed graph
the function which, given a weighted directed graph  with a distinguished vertex
with a distinguished vertex  called the root, returns a spanning tree rooted at
called the root, returns a spanning tree rooted at  of minimal cost.
of minimal cost.
The precise description is as follows. Given a weighted directed graph  with root
with root  we first replace any set of parallel edges (edges between the same pair of vertices in the same direction) by a single edge with weight equal to the minimum of the weights of these parallel edges.
we first replace any set of parallel edges (edges between the same pair of vertices in the same direction) by a single edge with weight equal to the minimum of the weights of these parallel edges.
Now, for each node  other than the root, mark an (arbitrarily chosen) incoming edge of lowest cost. Denote the other endpoint of this edge by
other than the root, mark an (arbitrarily chosen) incoming edge of lowest cost. Denote the other endpoint of this edge by 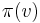 . If the marked edges form an SRT,
. If the marked edges form an SRT, 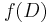 is defined to be this SRT. Otherwise, the set of marked edges form at least one cycle. Call (an arbitrarily chosen) one of these cycles
is defined to be this SRT. Otherwise, the set of marked edges form at least one cycle. Call (an arbitrarily chosen) one of these cycles  . We now define a weighted directed graph
. We now define a weighted directed graph 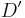 having a root
having a root 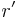 as follows. The nodes of
as follows. The nodes of 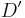 are the nodes of
are the nodes of  not in
not in  plus a new node denoted
plus a new node denoted 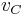 . If
. If 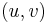 is an edge in
is an edge in  with
with 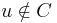 , include the edge
, include the edge  described below, in
described below, in 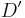 .
.
If 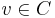 ,
, 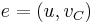 , and
, and 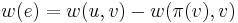 . Otherwise, if
. Otherwise, if 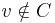 , let
, let 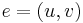 , and
, and 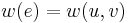 .
.
We include no other edges in 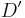 .
.
The root 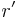 of
of 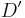 is simply the root
is simply the root  in
in  .
.
Using a call to 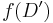 , find an SRT in
, find an SRT in 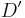 . Suppose in this SRT, the (unique) incoming edge at
. Suppose in this SRT, the (unique) incoming edge at 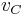 is
is 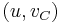 . This edge comes from some pair
. This edge comes from some pair 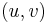 with
with 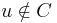 and
and 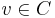 . Unmark
. Unmark 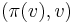 and mark
and mark 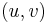 . Now the set of marked edges do form an SRT, which we define to be the value of
. Now the set of marked edges do form an SRT, which we define to be the value of 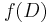 .
.
Observe that 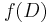 is defined in terms of
is defined in terms of 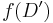 for weigthed directed rooted graphs
for weigthed directed rooted graphs 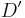 having strictly fewer vertices than
having strictly fewer vertices than  , and finding
, and finding 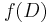 for a single-vertex graph is trivial.
for a single-vertex graph is trivial.
Implementation
Let BV be a vertex bucket and BE be an edge bucket. Let v be a vertex and e be an edge of maximum positive weight that is incident to v. Ci is a circuit. G0 = (V0,E0) is the original digraph. ui is a replacement vertex for Ci.
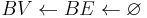 i=0
i=0
A:
if 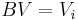 then goto B
for some vertex
then goto B
for some vertex 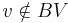 and
and 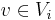 {
{
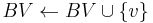 find an edge
find an edge 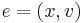 such that w(e) = max{ w(y,v)|(y,v)
such that w(e) = max{ w(y,v)|(y,v)  Ei}
if w(e) ≤ 0 then goto A
}
if
Ei}
if w(e) ≤ 0 then goto A
}
if 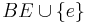 contains a circuit {
i=i+1
construct
contains a circuit {
i=i+1
construct 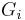 by shrinking
by shrinking 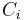 to
to 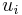 modify BE, BV and some edge weights
}
modify BE, BV and some edge weights
}
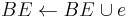 goto A
goto A
B:
while i ≠ 0 {
reconstruct 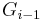 and rename some edges in BE
if
and rename some edges in BE
if 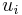 was a root of an out-tree in BE {
was a root of an out-tree in BE {
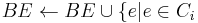 and
and 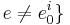 }else{
}else{
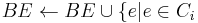 and
and 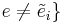 }
i=i-1
}
Maximum branching weight =
}
i=i-1
}
Maximum branching weight = 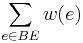
References
- Y. J. Chu and T. H. Liu, "On the Shortest Arborescence of a Directed Graph", Science Sinica, vol. 14, 1965, pp. 1396–1400.
- J. Edmonds, “Optimum Branchings”, J. Res. Nat. Bur. Standards, vol. 71B, 1967, pp. 233–240.
- R. E. Tarjan, "Finding Optimum Branchings", Networks, v.7, 1977, pp. 25–35.
- P.M. Camerini, L. Fratta, and F. Maffioli, "A note on finding optimum branchings", Networks, v.9, 1979, pp. 309–312.
- Alan Gibbons Algorithmic Graph Theory, Cambridge University press, 1985 ISBN 0-521-28881-9
- H. N. Gabow, Z. Galil, T. Spencer, and R. E. Tarjan, “Efficient algorithms for finding minimum spanning trees in undirected and directed graphs,” Combinatorica 6 (1986), 109-122.
External links
- The Directed Minimum Spanning Tree Problem Description of the algorithm summarized by Shanchieh Jay Yang, May 2000.
- Edmonds's algorithm ( edmonds-alg ) – An open source implementation of Edmonds's algorithm written in C++ and licensed under the MIT License. This source is using Tarjan's implementation for the dense graph.
- AlgoWiki – Edmonds's algorithm - A public-domain implementation of Edmonds's algorithm written in Java.